

But there’s no discernable pattern in the occurrence of the primes.
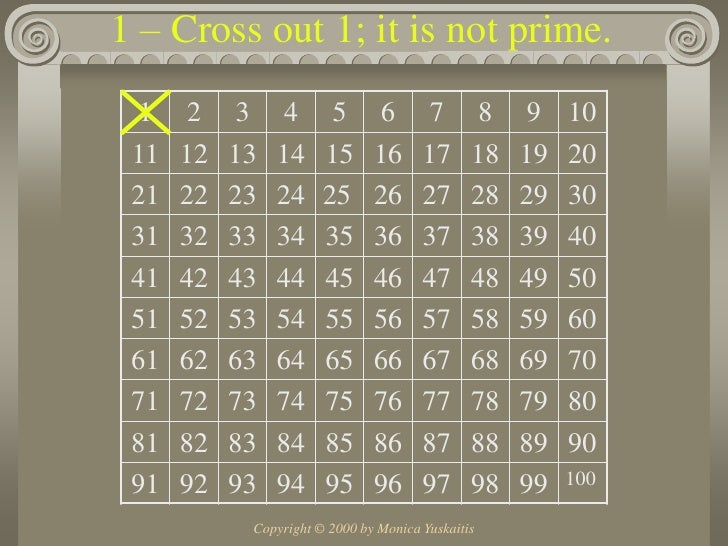
Not so randomĪ clear rule determines exactly what makes a prime: it’s a whole number that can’t be exactly divided by anything except 1 and itself. But, for mathematicians, it’s both strange and fascinating. “It’s a really nice result.”Īlthough prime numbers are used in a number of applications, such as cryptography, this ‘anti-sameness’ bias has no practical use or even any wider implication for number theory, as far as Soundararajan and Lemke Oliver know. “As soon as I saw the numbers, I could see it was true,” says mathematician James Maynard of the University of Oxford, UK. Prime numbers near to each other tend to avoid repeating their last digits, the mathematicians say: that is, a prime that ends in 1 is less likely to be followed by another ending in 1 than one might expect from a random sequence. “Every single person we’ve told this ends up writing their own computer program to check it for themselves,” says Kannan Soundararajan, a mathematician at Stanford University in California, who reported the discovery with his colleague Robert Lemke Oliver in a paper submitted to the arXiv preprint server on March 11. Two mathematicians have found a strange pattern in prime numbers-showing that the numbers are not distributed as randomly as theorists often assume.


 0 kommentar(er)
0 kommentar(er)
